To me the most valuable attribute of the Greeks is how they can be added, subtracted, or multiplied together across many different option contracts to see allow you to determine the overall impact of changes to a position or to your total portfolio.
Let’s jump in with some simple examples of how this works:
If you buy one contract at one strike price and sell another at a different strike price, what is the combined impact of a 1% increase in volatility? Let’s say the long contract has a Vega value of 0.15 and the short contract has a value of 0.10. The combined position Vega value can be found by subtracting the short values from the long values or in this case:
0.15 (long) – 0.10 (short) = 0.05 (combined)
So, if volatility goes up 1%, your combined position will go up 5 cents a share or $5 total.
Wait, you might say- how did we go from 0.05 to $5? You probably know the answer, there are 100 shares in an options contract. This is true for one contract. For multiple contracts just multiply by the number of contracts.
If you buy 5 option contracts that each have a Theta of -0.10, your position has a total Theta of -$50 (-0.10 x 5 x 100). This means your position is losing $50 every day due to time passing by based on time decay.
Hopefully, the math so far is simple for you. Let’s take it a step further by examining a combination of stock and options.
Security XYZ is trading for $200 per share and you decide to buy 300 shares of stock and at the same time sell 3 calls expiring in 42 days with a strike price of 207 for a premium of 2.40 per share on it. This combination transaction is a covered call. Let’s look at this from a Greek perspective:
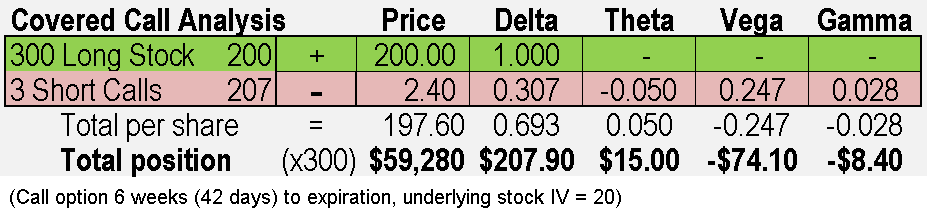
You can take several points from this quick analysis.
- The math for Greeks works for security shares as well as options.
- Buying or selling shares of stock have a major impact on the Delta of your position. Since Delta measures the movement of one share when the price goes up one dollar, the Delta is always 1.0 for a share of any security you own. However, time and volatility (Theta and Vega) don’t impact the stock.
- Since we are controlling 300 shares with each of these two positions, we can multiply the totals per share by 300 to see the position impact.
- While the call option was sold for just over 1% of the cost of the shares, it has a big Greek impact on the total position.
Why would anyone care about these numbers in combination you may ask? Because we can get a feel for what will happen to our total position if things change. For example, if the stock goes up a dollar tomorrow, we should gain $207.90 from price change (Delta), and $15 from one day’s time decay (Theta). If the stock price didn’t change, we’d still get the $15 from time passing. We’ll talk more about the merits of the covered call elsewhere, but hopefully you see how the Greek arithmetic works with a combination of stocks and options.
Now let’s examine a four option contract transaction, a combination of puts and calls, as well as long and short.
Security XYZ is trading for $200 per share and you decide to sell an Iron Condor with 42 days to expiration (a combination of buying one put while selling another put and also buying a call while selling another call). We’ll discuss the merits of spreads and Iron Condors elsewhere, but let’s focus for now on the math of the greeks to determine how to expect the total position to behave.
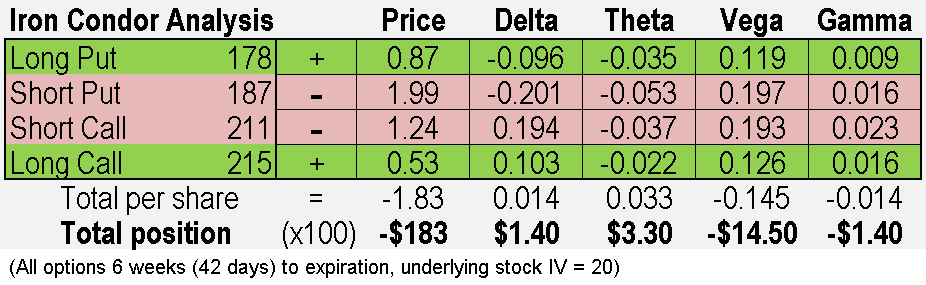
Some quick take-aways from this analysis:
- Since the options sold were more expensive than the ones purchased, there is a negative value for the total position. That’s correct, because selling means $183 cash in the account in exchange for being short overall for these four contracts.
- Each day the position will make $3.30 in time decay (Theta), which will make the value of the total position less negative.
- If the underlying stock goes up or down a dollar, it will only change the value of the total position by $1.40 (Delta)
- The value of the position could change a lot if volatility increases (Vega).
This position will do well if volatility stays the same or decreases over time, and the underlying price goes up a bit or stays the same. Since volatility generally goes up when prices drop, this position would lose some value from a price move down (Delta), but likely lose much more due to the increase in volatility (Vega).
Doing this math allows a trader to analyze a combination trade to make sure it has the performance characteristics desired before executing a trade and then to monitor going forward how the positions change in both value and greek components.
If all these computations give you a headache, and you have no desire to figure out the math, have no fear! Virtually all options trading platforms will display this math for you. The only challenge is to find the values in your broker platform and configure your display as a preference to view when you trade and when you review your positions overall. I know that my brokerage has all the Greeks totaled and available on its “trader” platform that is more advanced than the standard platform that most users access by default. If you have trouble getting this data easily, talk to your broker, or call their technical support.
To finish this section on Greek arithmetic, let’s look at what we get when we combine the two combination transactions we just reviewed together into a six-component portfolio:
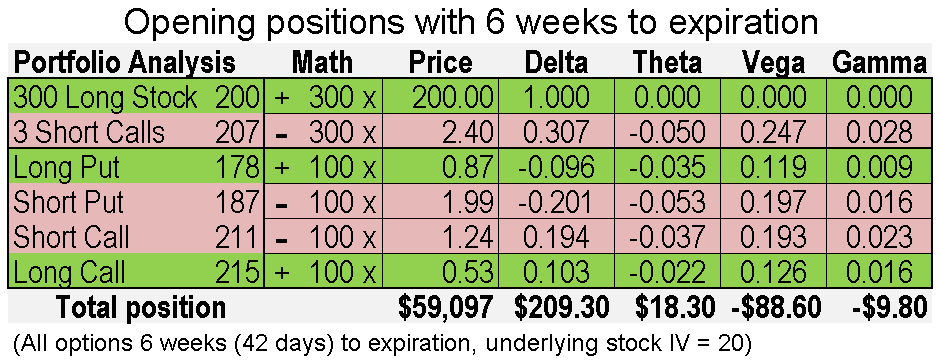
I added a little more detail with a math column so you can quickly see how each line is weighted based on its position (number of shares and short or long). When I look at this total position, I can quickly tell that it will be most impacted by price moves (Delta) and volatility moves (Vega). However, the total position will make money if the underlying stock does not change in price due to time decay (Theta).
As we learned earlier, over time stocks usually move up slowly and we could expect over three weeks that the stock would go up about 1%, if it hits the median of its range. If that happened, we would gain approximately $409 from the $2 underlying price move ($209 (Delta) + 209 -10 (Delta – Gamma)). We’d also collect 21 days of Theta (approximately $385). So, the median move would make almost as much from time decay than from price appreciation, even though at first glance Theta doesn’t look that big. The total move would be $794 if we assume vega has little impact. All these calculations are approximations- what I’d call back of the napkin calculations, since the greek values will change over time depending on the market environment and other factors (I rounded the numbers as well to the nearest dollar), but they should get you close. How close? Let’s look at this same total position three weeks later at 21 days to expiration:

The price of the stock went up $2, and the implied volatility changed to 19.5, likely a combination of increasing volatility skew as we move toward expiration countered by decreasing volatility from the market going up. But our option contracts have decayed quite a bit (Theta) along with the impact from the underlying price increase (Delta).
The difference in the value of the total position is $947, compared to my earlier estimate of $794. Not bad for back of the napkin. I didn’t take into account the fact that Theta increases as we approach expiration. Vega also helped a bit with volatility dropping slightly. The point is that you can predict roughly where your portfolio will go over time using the Greeks for different price moves.
You probably notice that the majority of the gain is due to the stock. So, why bother with options- didn’t they actually improve the return? Let’s do a quick check.
The math isn’t hard here. If we just bought 300 shares of stock and the price went up $2 a share, we’d make $600 profit instead of $947. We also would have paid a little more for stock alone to start ($60,000) to make less in this scenario.
What if the stock went down instead of up? Here’s the same position at the same time with the stock going down to $199.
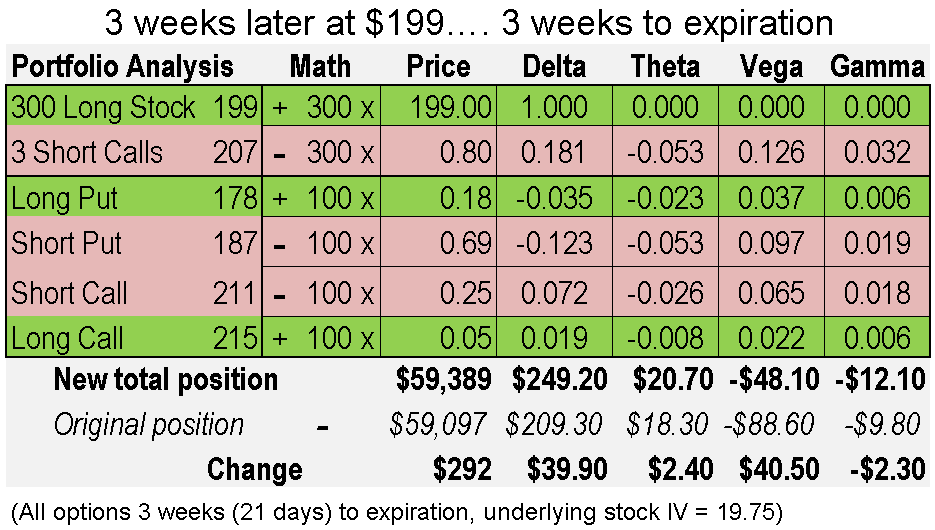
Notice that the position still went up in value, although not as much as when the stock went up. Why did it go up? Because Theta took away more time value from the option positions than Delta added from the price move. Also, since the underlying decrease was small, our implied volatility actually went down a tiny bit.
So, here is a position that we opened 6 weeks prior to expiration and in 3 weeks we can make money with the stock going up or down, even while we own the stock!
While the main point of these examples was to demonstrate the power of greek arithmetic, I want to point out two things you can take away from this example that I’m trying to emphasize throughout the site:
- Options can be much more capital efficient. The Iron Condor portion of this example required $900 in capital and could make $183 if the options expired worthless in 6 weeks. That’s over 20% return on capital. Our stock cost $60,000 and the median increase in 6 weeks would be less than 2%.
- When used correctly, options can actually reduce volatility of your position. You can set up positions that change less than an equivalent stock only portfolio while having the same or better return. If the expected move of the stock, based on the implied volatility, stays within one standard deviation, an option position similar to this example will outperform stock only
Now, let’s be clear- these examples are the median return and a very small price decline. There are lots of alternate situations that you can also expect to see where the options would have lost significant amounts. Elsewhere, we’ll look at those risks in detail and work through strategies to reduce risk as much as possible.